Matemáticas. Series de tempo
Actividade 2. A evolución das pernoitas nos establecementos de turismo rural

¿Crees que o turismo rural está cada vez máis de moda?

Existe a crenza de que cada vez máis xente opta por opcións alternativas á hora de escoller o tipo de aloxamento para pasar as súas vacacións. Neste exercicio tratarase de comprobar a veracidade desta afirmación a partir dos datos que facilita o IGE.

Número de pernoitas nos establecementos de turismo rural en Galicia

	2017	2018	2019	2020	2021	2022	2023	2024
Xaneiro	7.865	7.288	7.996	6.073	1.261	4.948	5.723	6.272
Febreiro	8.834	10.602	9.985	8.218	768	7.325	7.214	6.972
Marzo	11.589	23.106	13.728	2.092	5.365	8.316	9.399	18.955
Abril	38.374	20.989	34.363	0	9.850	31.395	29.2493	20.029
Maio	28.002	30.907	35.974	220	12.695	31.762	26.838	33.857
Xuño	38.842	37.725	40.696	7.619	19.723	36.225	35.986	36.978
Xullo	76.076	60.792	67.151	41.105	64.165	67.926	65.312	60.976
Agosto	119.170	109.451	112.514	78.008	108.044	104.780	105.191	101.063
Setembro	51.345	49.463	46.391	23.043	44.164	44.132	43.755	48.041
Outubro	33.456	33.379	27.544	10.922	32.171	28.837	27.491	27.177
Novembro	14.563	16.856	13.564	2.293	14.479	13.908	11.539	12.822
Decembro	20.924	17.555	17.138	2.531	15.360	16.045	18.138	12.014

Na representación gráfica da serie pódese observar unha tendencia lixeiramente crecente no número de pernoitas durante os anos posteriores á crise económica ata o ano 2020, no que debido a crise da pandemia do coronavirus, prodúcese un desplome nas pernoitas. A partires do 2021 obsérvase unha recuperación das cifras de pernoita pero sen acadar as cifras do 2019. Polo outro lado obsérvase unha forte estacionalidade anual. O maior número de pernoitas dáse nos meses de verán, sobre todo en agosto. Ademais, tamén se observan uns pequenos picos nos meses de marzo-abril, posiblemente debidos a que a Semana Santa cadra nalgúns destes meses. Desta representación gráfica tamén se desprende que o menor número de pernoitas se produce nos dous primeiros e nos dous últimos meses do ano.

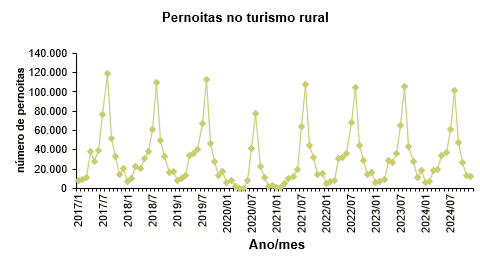
¿Como evolucionan as pernoitas do turismo rural a longo prazo?

Para illar o movemento da serie a longo prazo (tendencia) dos outros elementos que a compoñen usaranse dou métodos: o método de axuste analítico e o método das medias móbiles.

Método de axuste analítico para a análise da tendencia

Neste método tratarase de axustar unha función que relacione o número de pernoitas anuais en función do tempo. Esta función deberá recoller a marcha ou a evolución xeral da serie.

Neste exemplo axustarase a tendencia da serie de pernoitas a unha recta (f(t)=a₀+b₀t) mediante o método de mínimos cadrados. Para este axuste os parámetros a₀ e b₀ veñen determinados pola seguinte expresión:

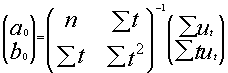
Ano	t	t2	Total de pernoitas anuais (ut)	t*ut
2017	1	1	449.040	449.040
2018	2	4	418.113.	836.226
2019	3	9	427.044	1.281.132
2020	4	16	182.124	728.496
2021	5	25	328.046	1.640.230
2022	6	36	395.600	2.373.600
2023	7	49	385.333	2.697.331
2024	8	64	385.186	3.081.488
n=8 (anos)	St=36	St2=204	Sut=2.970.486	St*ut=13.087.543

Se se substitúen na fórmula os datos do exemplo das pernoitas anuais, obteríanse os seguintes valores para os coeficientes do modelo:

Polo tanto, o axuste linear da tendencia da serie vén dado por f(t)=401.272,6 - 6.658,2t

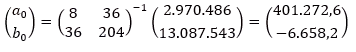
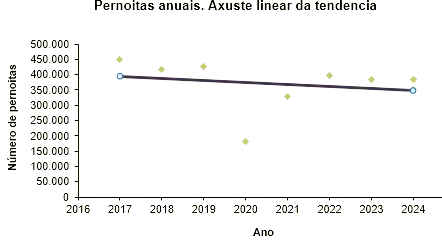
Neste exemplo parece que o modelo linear non é suficiente para axustar a tendencia da serie, obtéñense melloras significativas utilizando o axuste parabólico. O axuste linear ten unha forma decrecente, mentras que o parabólico amosa unha tendencia decrecente nos primeiros anos da serie e outra crecente nos últimos anos do período 2017-2024.

Método das medias móbiles para a análise da tendencia

Tal e como se pode observar na gráfica do número de pernoitas no turismo rural, trátase dunha serie mensual con estacionalidade anual, polo que se debe considerar p=12. Dado que p é par, primeiro hai que calcular as medias móbiles de orde p-1=11 e p+1=13.
Por exemplo, para o mes de xullo de 2017 para calcular a media móbil de orde 11 considéranse os datos dos meses comprendidos entre febreiro de 2017 e decembro de 2017 (ambos os dous incluídos) e calcúlase a media dos seus valores. Logo, tómanse os meses desde xaneiro de 2017 ata xaneiro de 2017 e calcúlase a correspondente media móbil de orde 13. Finalmente, para calcular a media móbil de orde p=12, considéranse as dúas medias anteriores e calcúlase a súa media.
Operando deste xeito, obtéñense as seguintes medias móbiles de orde 12 para a serie mensual do número de pernoitas.

Medias móbiles de orde 12

	2017	2018	2019	2020	2021	2022	2023	2024
Xaneiro	-	36.319	35.923	24.419	18.017	33.124	33.155	32.480
Febreiro	-	34.950	35.990	21.590	19.963	32.863	31.794	31.846
Marzo	-	34.910	36.430	19.586	22.525	33.160	32.222	32.253
Abril	-	34.946	36.179	18.018	24.387	33.114	32.260	32.549
Maio	-	35.163	35.903	16.926	25.882	33.064	32.213	32.696
Xuño	-	35.093	35.732	15.827	26.927	33.059	32.170	32.472
Xullo	37.604	35.063	35.706	15.056	27.661	33.192	32.359	-
Agosto	37.639	35.048	35.706	14.535	28.084	33.207	32.364	-
Setembro	38.144	34.572	34.983	14.365	28.464	33.236	32.705	-
Outubro	37.811	34.675	32.988	14.908	29.395	33.042	32.646	-
Novembro	37.205	35.408	30.039	15.834	31.088	32.752	32.514	-
Decembro	37.218	35.705	27.109	16.814	32.540	32.488	32.807	-

¿Como oscila o número de pernoitas durante o ano?

As oscilacións que normalmente se producen cun período igual ou inferior ao ano e que son recoñecibles nos diferentes anos son as variacións estacionais. O motivo principal que leva a estudar a compoñente estacional é que, en moitas das series temporais, a dita compoñente provoca unha distorsión do verdadeiro movemento da serie. Polo tanto, para estudar a evolución dunha variable e captar o seu movemento real, o primeiro que se debe facer é eliminar a compoñente estacional. Neste exemplo utilizarase o método das relacións medias mensuais con respecto á tendencia e o método das medias móbiles.

Método das relacións medias mensuais con respecto á tendencia

1. O primeiro paso é axustar as medias anuais dos datos a unha recta a₀+b₀t polo método de mínimos cadrados. Procedendo de maneira similar a cando se calcula o axuste linear da tendencia tense:
   
   

   Ano	t	t2	Media anual das pernoitas (ut)	t*ut
   2017	1	1	37.420	37.420
   2018	2	4	34.843	69.686
   2019	3	9	35.587	106.761
   2020	4	16	15.117	60.708
   2021	5	25	27.337	136.685
   2022	6	36	32.967	197.800
   2023	7	49	32.153	225.070
   2024	8	64	32.096	256.771
   n=8 (anos)	St=36	St2=204	Sut=247.580	St*ut=1.090.901

   
   Polo tanto, o axuste linear para a media anual das pernoitas vén dado por f(t)=33.434-553t
2. O seguinte paso é calcular as medias mensuais dos datos (x_·j).
3. Corríxense as medias mensuais ao lle restar a cada media mensual a parte proporcional do incremento anual (b₀). As medias mensuais corrixidas denotaranse por: x'_·j.
4. Obtense a media global corrixida como a media aritmética das medias mensuais corrixidas(x'..).
5. O ultimo paso é obter a compoñente estacional. Se supoñemos que o modelo é multiplicativo, o índice de variación estacional (en tanto por un) viría dado polo cociente entre a correspondente media mensual corrixida e a media global corrixida (x'_·j/x'..)

Todos os cálculos anteriores se poden resumir na seguinte táboa:

Mes	Media mensual (x·j)	Media mensual  corrixida (x'·j)	Índice de variación  estacional (x'·j/x'..)
Xaneiro	5.928	5.928	0,190
Febreiro	7.490	7.536	0,242
Marzo	11.569	11.661	0,374
Abril	23.031	23.169	0,743
Maio	25.032	25.216	0,808
Xuño	31.724	31.954	1,024
Xullo	62.938	63.214	2,026
Agosto	104.778	105.100	3,369
Setembro	43.792	44.160	1,415
Outubro	27.622	28.037	0,899
Novembro	12.503	12.963	0,415
Decembro	14.963	15.470	0,496
		x'..=31.201

Na gráfica anterior pódese observar como os meses de verán (sobre todo agosto) teñen unha marcada tendencia alcista, mentres que os meses de xaneiro e febreiro son nos que o número de pernoitas cae de maneira máis drástica.

Método das medias móbiles

Para este método os pasos que se van seguir pódense resumir do seguinte xeito:

1. Calcular a compoñente extraestacional(E_ij) facendo un axuste da serie orixinal (x_ij) mediante o método das medias móbiles con p=12. Este paso xa se realizou anteriormente ao axustar a tendencia mediante o método das medias móbiles.
2. Unha vez calculada a compoñente extraestacional, e se supón que o modelo é multiplicativo, obtense a compoñente estacional (s_·j) para todos os meses (j=1, ..., 12) aplicando a seguinte fórmula:

   

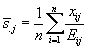
Mes	Compoñente estacional modelo multiplicativo
Xaneiro	0,190
Febreiro	0,242
Marzo	0,374
Abril	0,743
Maio	0,808
Xuño	1,024
Xullo	2,026
Agosto	3,369
Setembro	1,415
Outubro	0,899
Novembro	0,415
Decembro	0,496

Para acceder a todos os cálculos realizados na folla de cálculo Excel picar no seguinte aderezo Ver cálculos

Actividades complementarias

1. No seguinte enlace podes descargar os datos das pernoitas no turismo rural para as catro provincias galegas: Pernoitas por provincias
   Trata entón de responder as seguintes preguntas:
   • ¿A evolución das pernoitas no turismo rural segue o mesmo patrón nas catro provincias galegas?
   • ¿En cal das catro provincias a serie do número de pernoitas ten unha tendencia crecente máis marcada?
   • Ao longo do ano ¿O número de pernoitas oscila de igual xeito en todas as provincias?
2. Se picas aquí podes descargar a serie do número de pernoitas nos establecementos hoteleiros (hoteis+hostais) de Galicia.
   • ¿De que maneira están correlacionadas as pernoitas que se rexistran durante un ano coas que se produciron nos anos anteriores?
   • ¿Ten a serie unha tendencia crecente tan marcada como a das pernoitas no turismo rural?
   • Estuda como varía o número de pernoitas durante os meses do ano.